matlab中函数svd是什么意思

奇异值分解 (sigular value decomposition,SVD) 是一种正交矩阵分解法；SVD是最可靠的分解法，但是它比QR 分解（QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵。）法要花上近十倍的计算时间。

[U,S,V]=svd(A)，其中凯做U和V代表二个相互正交矩阵，而S代表一对角矩阵。 和QR分解法相同者， 原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。

函数 svd

格式 s = svd (X) %返族乱回矩阵X 的奇异值向量

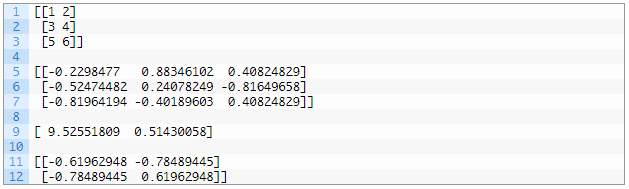
[U,S,V] = svd (X) %返回一个与X 同大小的对角矩阵S，两个酉矩阵U 和V，且满足= USV’。若A 为m×n 阵，则U 为兆孙档m×m 阵，V为n×n 阵。奇异值在S 的对角线上，非负且按降序排列。

[U,S,V] = svd (X,0) %得到一个“有效大小”的分解，只计算出矩阵U 的前n列，矩阵S 的大小为n×n。

扩展资料

使用误区

>> S=svd(A)

??? Undefined function or method 'svd' for input arguments of type 'uint8'.

出错原因，A的数据类型为uint8

解决办法S=svd（double（A））

>> S=SVD(double(A))

??? Undefined function or method 'SVD' for input arguments of type 'double'.

出错原因，SVD在R2011a中不能被调用，区分大小写

解决办法S=svd（double（A））

标签：matlab,svd,函数