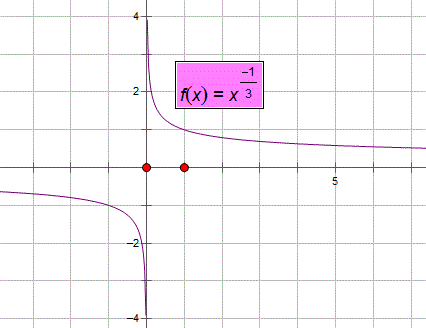
1 当a为负数时,定义域为(-∞,0)和(0,+∞);
2 当a为零时,定义域为(-∞,0)和(0,+∞);
3 当a为正数时,定义域为(-∞,+∞)。
4 在(x2-2x)^(-0.5))^(-0.5)中,首先解x2-2x≠0,解出x≠0且x≠2,因此定义域为(-∞,0)∪(0,2)∪(2,+∞)。
当a为不同的数值时,幂函数的定义域的不则袜蚂同情况如下:
1 如果a为任意实数,则函数的定义域为大于0的所有实数;
2 如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根[据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;
3 如果同时q为奇数,则函数的定义域为不等于0的所有实数。
扩展资料:
对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:
1 如果a=p/q,q和p都是整数,则x^(p/q)=q次根号(x的p次方),
2 如果q是奇数,函数的定义域是R,
3 如果q是偶数,函数的定义域是[0,+∞)。
4 当指数n是负整数时,设a=-k,则x=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞).
单调区间:
当α为整数时,孙埋α的正负性和奇偶性决定了函数的单调性:
①当α为正奇数时,图像在定义域为R内单调递增;
②当α为正偶数时,图像在定义域为第二象限内单调递减,好差在第一象限内单调递增;
③当α为负奇数时,图像在第一三象限各象限内单调递减(但不能说在定义域R内单调递减);
④当α为负偶数时,图像在第二象限上单调递增,在第一象限内单调递减。
当α为分数时,α的正负性和分母的奇偶性决定了函数的单调性:
①当α>0,分母为偶数时,函数在第一象限内单调递增;
②当α>0,分母为奇数时,函数在第一、三象限各象限内单调递增;
③当α<0,分母为偶数时,函数在第一象限内单调递减;
④当α<0,分母为奇数时,函数在第一、三象限各象限内单调递减(但不能说在定义域R内单调递减);
参考资料:百度百科——幂函数
标签:幂函数,定义域