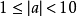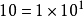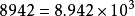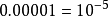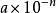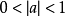积的乘方，先把积中的每一个乘数分别乘方，再把所得的幂相乘。可以简记为，积的乘方等于乘方的积。
用字母表示为：（a×b）^n＝a^n×b^n
这个积的乘方法则也适用于三个以上乘数积的乘方。如：
（a×b×c）^n＝a^n×b^n×c^n
aM次方与aN次方相乘，（M，N为正整数）
自主探究：将式子反转后也可称为“同指数幂乘法”
即：同指数幂相乘，指数不变，底数相乘。a^n*b^n=（ab）^n
求n个相同因数乘积的运算，叫做乘方，乘方的结果叫做幂(power)。其中，a叫做底数(base number)，n叫做指数(exponent)。当aⁿ看作a的n次乘方的结果时，也可读作“a的n次幂”或“a的n次方”。
一个数都可以看作自己本身的一次方，指数1通常省略不写。在写分数和负数的n次方时要加括号。四则运算顺序：先乘方，再括号（先小括号，再中括号，最后大括号），接乘除，尾加减。
计算一个数的小数次方，如果那个小数是有理数，就把它化为 （即分数）的形式。特别的，除0以外的任何数的0次方均等于1。0的非正指数幂没有意义。
向左转|向右转
扩展资料：
一个绝对值大于等于1的数可以写成
向左转|向右转
（其中，
向左转|向右转
，且n为正整数）的形式叫做科学记数法 例如：
向左转|向右转
、
向左转|向右转
当是负整数指数幂的时候，绝对值小于1的数也可以用科学记数法表示。例如：
向左转|向右转
，即绝对值小于1的数也可以用科学记数法表示为
向左转|向右转
的形式，租伏其中
向左转|向右转
，
向左转|向右转
是正整数。
任何非0实数的0次方都等于1。
有理数乘方的符号法则：
（1）负数的偶次幂是正数，负数的奇数幂是负数。
（2）正数的任何次幂都是正数。
（3）0的任何正数次幂都是0。
求n个相同因数乘积的运算，叫做乘方，乘方的结果叫做幂(power)。其中，a叫做底数(base number)，n叫做指数(exponent)，当aⁿ看作a的n次乘方的结果时，也可读作“a的n次幂”或“a的n次方”。
注：下面的讨论中，底数均不为0。
乘积的概念取决于“乘法”概念的定义。 当人们将乘法的对象集合提升为更一般慎型耐的集合，诸如群、环、域等时， 乘积的概念也将有所变化。
设A是一个集合， 我们定义乘法F:A ×A→A, 即一个从A与自身的笛卡尔积到A的映射。 设(x,y)∈A×A， 那么我们称像元素F(x,y)为x和y的乘积， 简记为xy。
乘积是数学中多个不同概念的称呼。宽春算术中，两个数或多个数相乘得到的结果称为它们的积或乘积。当相乘的数是实数或复数的时候，相乘的顺序对积没有影响，这称为交换性。
当相乘的是四元数或者矩阵，或者某些代数结构里的元素的时候，顺序会对作为结果的乘积造成影响。这说明这些对象的乘法没有交换性。
当相乘的对象多于两个的时候，常常使用连乘号∏（大写的π）表示。就如同多个对象的加法使用∑作为符号一样。一般约定，相乘的对象只有一个的时候，乘积是对象本身；没有相乘的对象时也可以约定所谓的“空积”为1。
标签：是积,乘方
