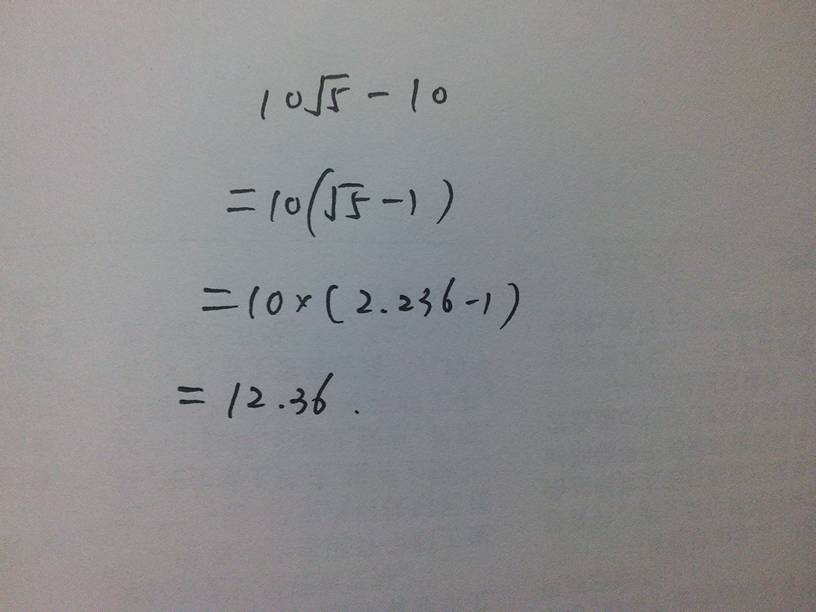根号5怎么计算

√5≈2.2360或-2.2360。

可用算术平方根的笔算方法求出。

先判定2＜√5＜3，设（2+a)=√5，则4+4a+aa=5，a(4+a)=1，a≈1/4，故√5的十分位为2，再设（2.2+b)=√5，则4.84+4.4b+bb=5，b(4.4+b）=0.16，b≈0.16÷4.4，故√5的百分位为3。

√5是一个无理数，用这样的方法永远求不出精确好锋值，所以根据需要保留几位小数就可以了。

求算术平方根，一般先把被开方数从小数点起两位分为一友闭晌节（每节对应根的一位）,用一个类似除法竖式符号（根号），从高到低一位一位求出来。

扩展资料：

如果一个非负数x的平方等于a，即 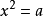 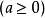，  ，那么这个非负数x叫做a的算术平方根。a的算术平方根记为  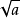，读作“根号a”，a叫做被开方数（radicand）。求一个非负数a的平方根的运算叫做开平方。

结论：被开方数越大，对应的算术平方根也越大（对所有正数都成立）。

一个正数如果有平方根，那么必定有两个，它们互为相反数。显然，如果知道了这两个平方根的一个，那么就可以及时的根据相反数的概念得到它的另一个平方根。

负数在实数系内不能开平方。只有在复数系内，负数才可以开平态兄方。负数的平方根为一对共轭纯虚数。例如：-1的平方根为±i，-9的平方根为±3i，其中i为虚数单位。规定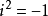：  ，或 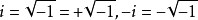 。一般地，“√￣”仅用来表示算术平方根，即非负数的非负平方根。

规定：0的算术平方根为0。

参考资料：百度百科---平方根

标签：根号,计算