向量的数量积公式:a*b=|a||b|cosθ a,b表示向量,θ表示向量a,b共起点时的夹角,很明显向量的数量积表示数,不是向量。
一个向量和另个向量在这个向量上的投影的乘积,前提始位置要相同。
已知两个非零向量a、b,那么|a||b|cosθ(θ是a与b的夹角)叫做a与b的数量积或内积。记作a·b。
两个向量的数量积等于它们对应坐标的乘积的和。
即:若a=(x1,y1),b=(x2,y2),则a·b=x1·x2+y1·y2
向量的数量积公式:a*b=|a||b|cosθ,a,b表示向量,θ表示向量a,b共起点时的夹角,很明显向量的数量积表示数,不是向量。 一个向量和另个向量在这个向量上的投影的乘积,前提始位置要相同。
拓展资料
平面向量数量积
已知两个非零向量a、b,那么|a||b|cosθ(θ是a与b的夹角)叫做a与b的数量积或内积。记作a·b。两个向量的数量积等于它们对应坐标的乘积的和。
即:若a=(x1,y1),b=(x2,y2),则a·b=x1·x2+y1·y2
性质
设 a、b为非零向量,则
①设 e是单位向量,且 e与 a的夹角为θ,则 e·a= a·e=| a|| e|cosθ
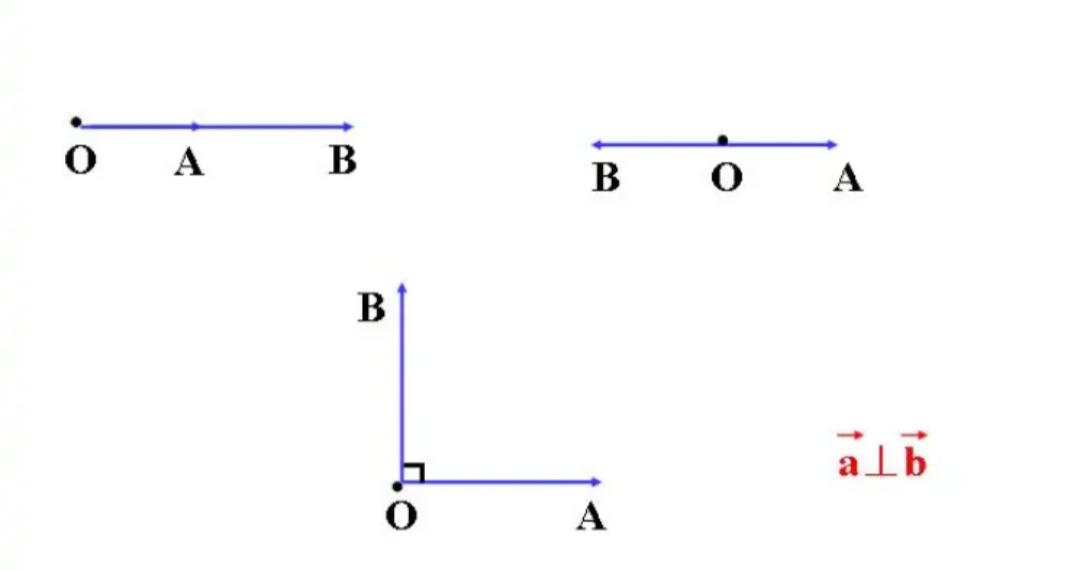
② a⊥b= a·b=0
③当 a与 b同向时, a·b=| a|| b|;当 a与 b反向时, a·a=| a|= a或| a|=√ a·a
④|a·b|≤|a|·|b|,当且仅当a与b共线时,即a∥b时等号成立
⑤cosθ=a·b╱|a||b|(θ为向量a.b的夹角)
⑥零向量与任意向量的数量积为0。
运算
⑴交换律: a·b= b·a
⑵数乘结合律:( λa)· b= λ( a·b)= a·( λb)
⑶分配律:( a+b)· c= a·c+ b·c
几何意义
①一个向量在另一个向量方向上的投影
设θ是a、b的夹角,则|b|cosθ叫做向量b在向量a的方向上的投影,|a|cosθ叫做向量a在向量b方向上的投 影。
② a·b的几何意义
数量积 a·b等于 a的长度| a|与 b在 a的方向上的投影| b|cosθ的乘积
★注意:投影和两向量的数量积都是数量,不是向量。
③数量积 a·b的几何意义是: a的长度| a|与 b在 a的方向上的投影| b|cos θ的乘积。
求向量的模的方法
公式法,利用|a|=及(a±b)2=|a|2±2a·b+|b|2,把向量的模的运算转化为数量积运算;
(2)几何法,利用向量的几何意义.
请点击输入图片描述
求向量模的最值(范围)的方法:
代数法,把戚毁弯所求的模表示成某个变量的函数,再用求最值的方法求解;
(2)几何法(数形结合法),弄清所高闷求的模表示的几何意义,结合动点表示的余姿图形求解.
标签:向量,公式,数量